Let’s start out this week with a little brain teaser type problem.
How would you calculate the rotation angle for the minute and hour hand of a clock?
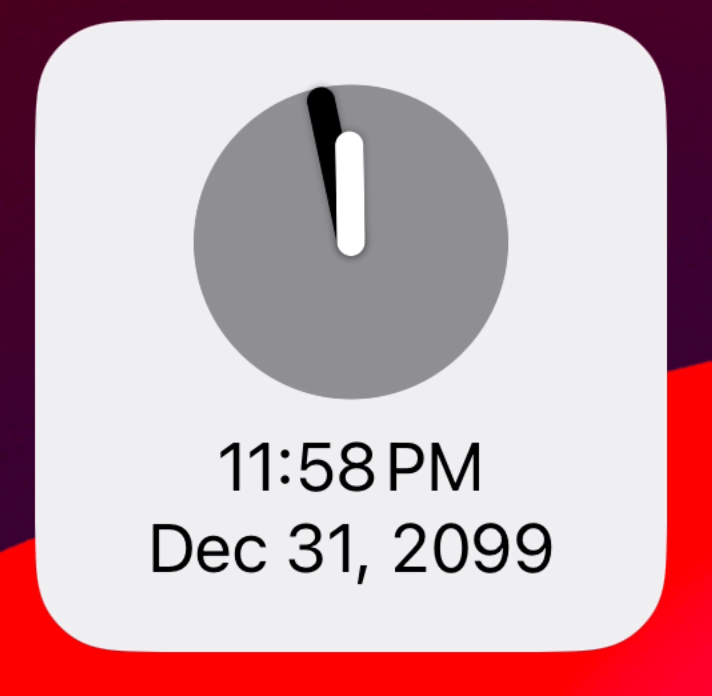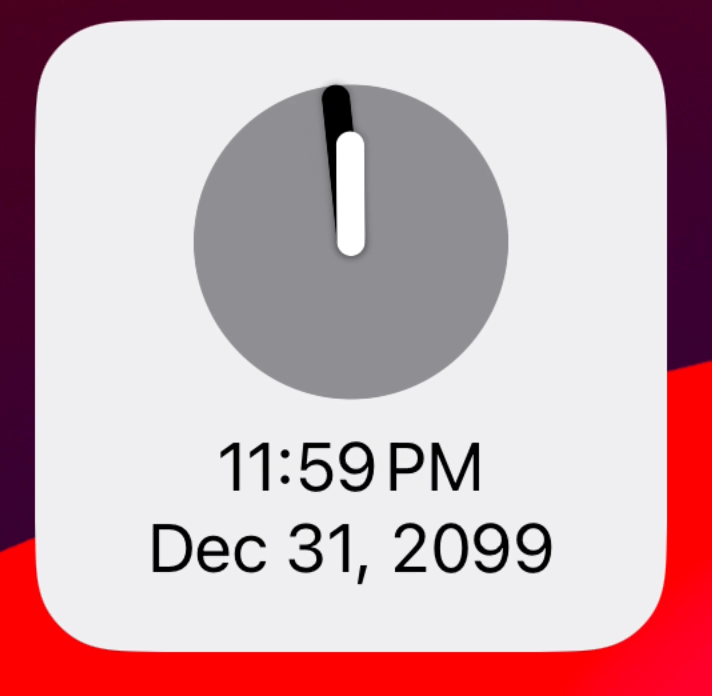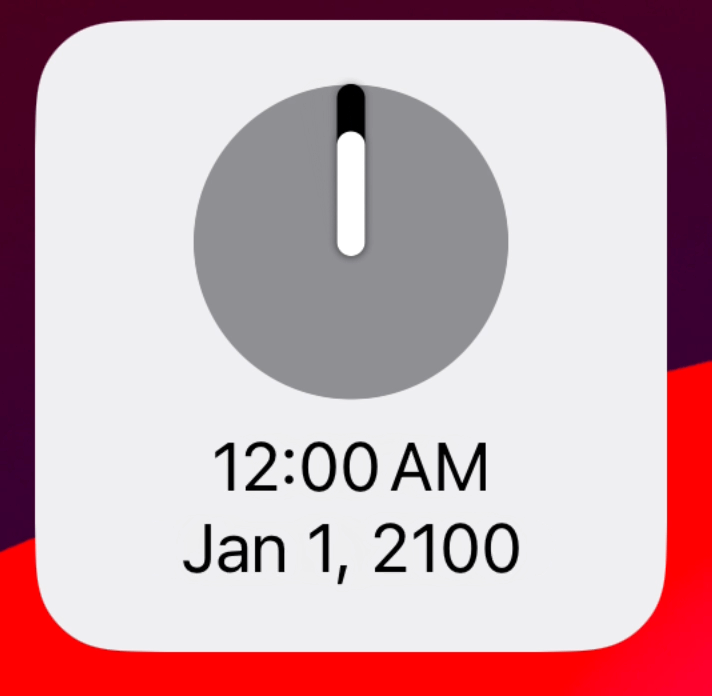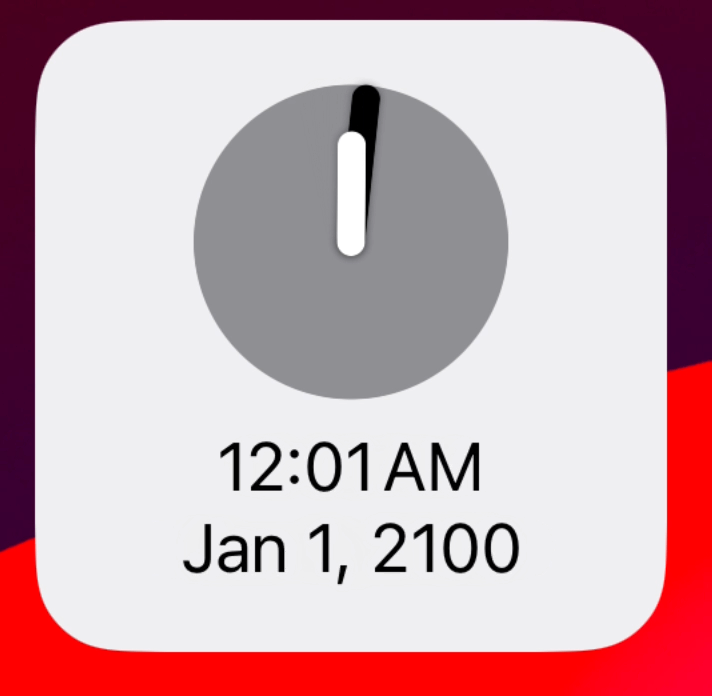
Specifically this came to mind for me because of a feature in Widgetsmith where you can specify an analog clock as one of your widgets which looks like this.

I’d encourage you to pause for a moment and actually think how you’d approach this because the result I ended up with was way more complex than I would have initially guessed and it was a good learning exercise to reason through.
The version of this feature which shipped with iOS 17 used the rotation angle calculation I had used since Widgetsmith was first created which is based on a simple method dividing a full rotation of the clock hands by the current hour/minute.

This worked fine in the old version of WidgetKit which only showed one widget at a time, but starting in iOS 17 each progressive widget refresh is now animated between the previous and next value. So now at the end of every hour you get this:

Not great, because I’m only calculating each rotation based on a single rotation around the clock face it jumps from 360° back to 0°.
OK I thought let’s adjust the minute so that it takes into account the hour of the day as well and successfully add in an additional 360° rotation at the start of each hour.


That solves the minute hand jumping around during the day, but now at midnight we have this:

Now at midnight we get a massive backwards rotation because we are again reverting to 0° at the start of each day.
So my next thought is that we need to instead try and make the rotation increase continuously (monotonically for the mathematically inclined). That way the rotation will just keep rolling around and around over time.
This was my first attempt at this type of approach where I pick an arbitrary anchor date and then calculate the number of seconds since that date and then just keep rotating based on the number of hours/minutes it has been since then.

This gets around the midnight reset problem. Though it does mean that I am now providing rotations way outside of the typical 360° range so I wanted to then check if this would eventually overflow and cause issues with the renderer. But trying it with a date far into the future seems to work just fine.
But now the next problem I face is a bit more subtle and relates to the spectre which haunts all programming work which relates to time, daylight savings. Because this approach starts its rotation at midnight on New Year’s Day and then increases linearly from there it will fall apart when the clocks change.

I’m not accounting for the fact that there can be instances where the rotation angle isn’t actually evenly increasing between each date. It needs to either jump forward or backwards when the daylight savings points are met.
My first thought for how to solve this problem would be to determine the starting angle of each day and then use that as the reference point to adjust then based on the previous hour/minute method. This way I’m determining the daily rotation based on the actual hour/minute value (2pm, 4:12am, …) and not just the time since the reference.
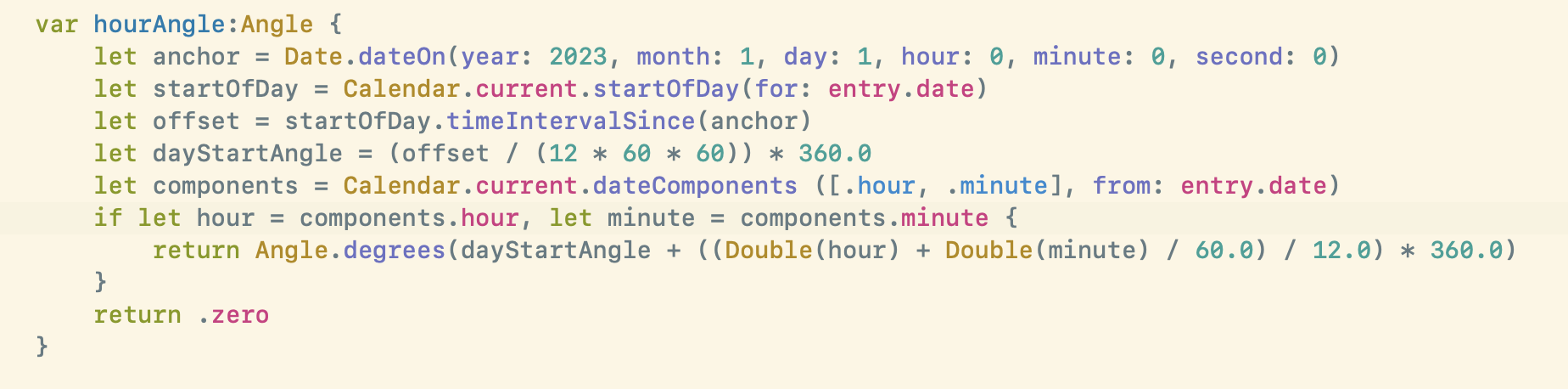
This approach however includes a subtle bug. Can you spot it? The issue comes from the fact that the start of each day isn’t actually a multiple of 24 hours from the start of the year…because in March when the clocks change we have a non 24 hour day. 🤦🏻♂️
So taking this approach I would get funny rendering bugs after March.

But I think I was on the right path by referencing the start of each day as my baseline for then adjusting a daily rotation. But instead of basing it on the number of seconds from the start of the year I need to instead determine the number of whole days and then multiply that out to get how many full daily rotations have occurred.
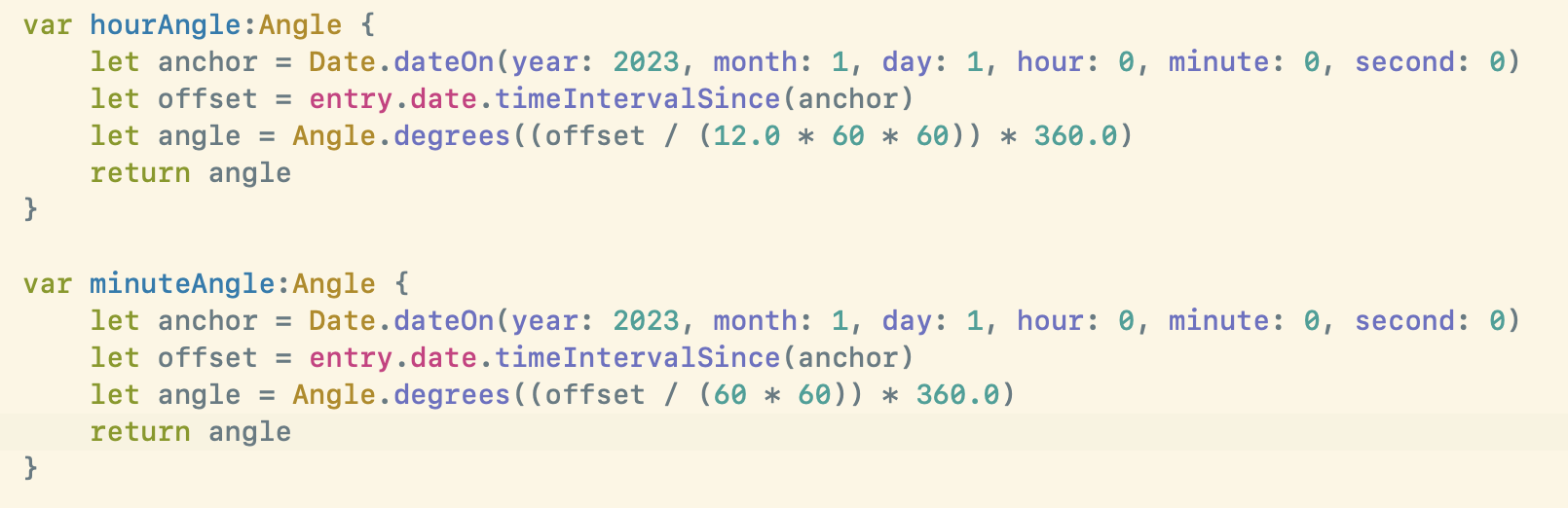
This is what I ended up with (code here):

Here I use the number of full rotations of each of the hands per day as the basis for my calculations (2 for the hour hand and 24 for the minute hand).
Then determine the number of whole days have past since my anchor date, and multiply this by the revolutions per day.
Now I have the correct starting point from which I can then determine how far to rotate based on the nominal hour and minute values in the current timezone. Then I’m adding these two values together to get the final rotation.
As far as I can tell this works perfectly. I’m still doing a bit more testing to be sure but here is for example what it does at the two daylight savings points:

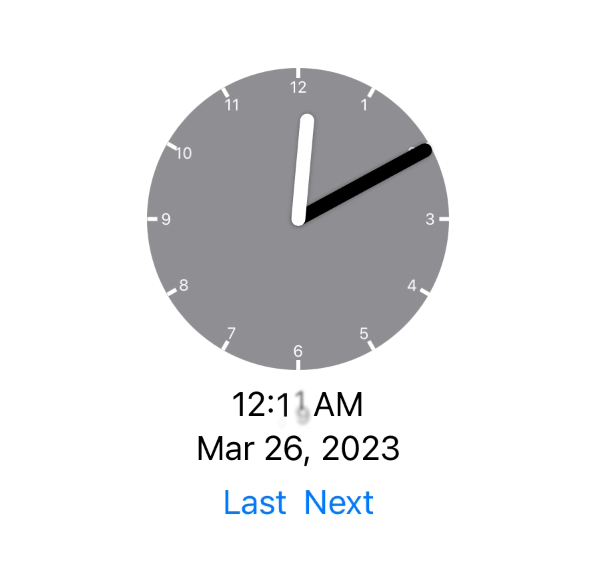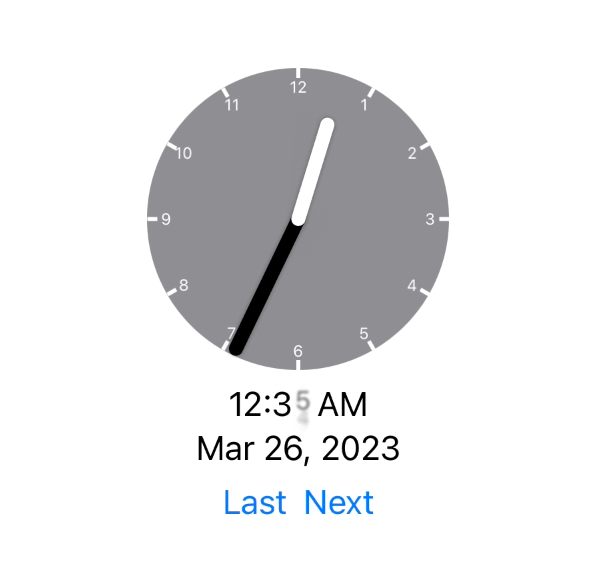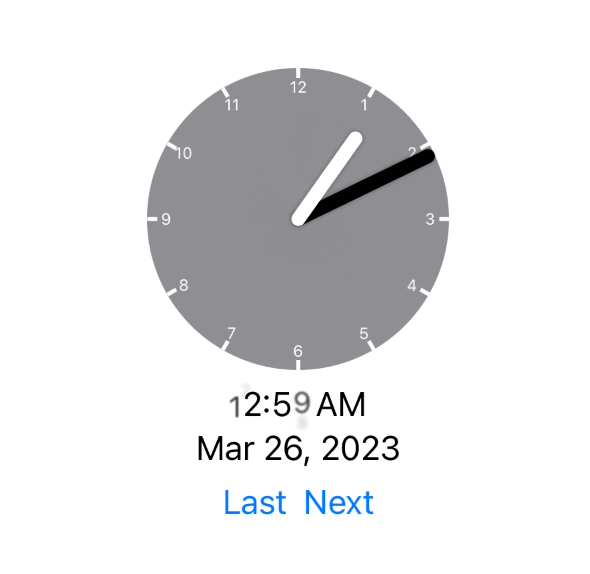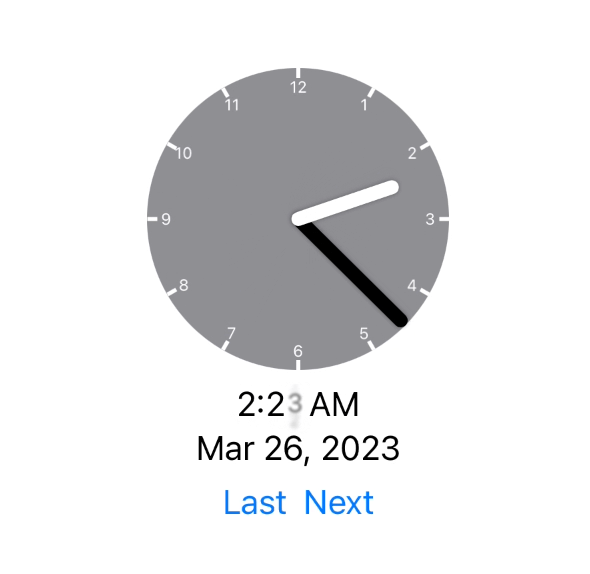
The animation actually now involves the correct adjustment being made (either jumping forward or falling behind).
Code like this is always an interesting challenge to get right. Personally I find it very difficult to think through all the possibilities and ensure that I’m accounting for all the correct factors.
I hope this approach is right (if you see a bug in my logic please do let me know!), but either way I’ve learned a bunch for the process of thinking it through which was a great way to start out my week.